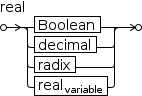
2.3.2 Numbers and Other Values

A value (Figure 2.11) is denoted by a syntactic form called a literal that determines the value's type, representation and content.

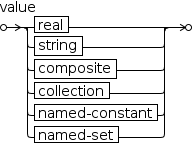
2.3.2.1 Numeric

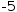
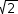
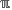
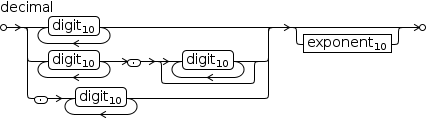
Numeric values represent magnitude. Simple numeric values are stored internally using 64-bit IEEE representation with about sixteen digits of base-10 precision. Other numeric values include rational numbers like -5 and 4/3, irrational numbers like √2, transcendental numbers like ℼ and cos 0 and the imaginary number ⅉ. Some of these values can only be approximated by the internal representation. Others cannot be represented at all and are retained in symbolic form. In this guide, the term real is used for numeric values.

Simple numbers (Figure 2.13) are entered as a sequence of decimal digits containing at most one decimal point. A negative number is represented by a manifest expression: the negation of a non-negative number. Scientific notation is supported: a simple number can be followed by the letter E and an optionally signed integer representing the power of 10 to which the number is to be raised.

(a) Decimal

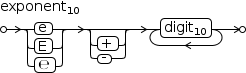
(b) Exponent

To keep the display clean, numbers with fractional parts are displayed with at most three digits of precision. Scientific notation with at most three digits of precision is used if a real value cannot be displayed within this constraint. Although the display might not present the complete value, the text-output area always contains the number with the maximum precision. A number with a large number of digits in the fraction like the left operand in 1.23456^10 will display as 1.23^10. Evaluated, the number of fraction digits increases; the expression evaluates to 8.224736938276754, but displays as 8.22.

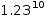
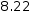
(a) radix

(d) ɽ-Exponent

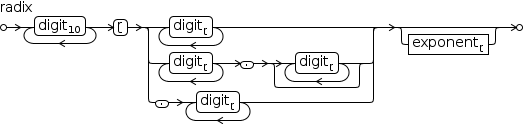
Number bases other than 10 use the notation given in Figure 2.14. A number with a non-decimal base is written starting with the base (in decimal) followed by the radix symbol “ɽ” (or “r”) followed by the number using radix-ɽ digits. Radix-ɽ digits include any digit ranging from 0 up to but not including the base. Digits beyond 9 are taken from the aphabet, starting with A for 10 and ignoring case. For example, a hexadecimal integer is entered as 16ɽ12AB and displays as 16ɽ12AB.

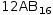
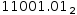
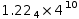
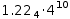
Radix numbers can also contain a radix point. For example, 25.25 in binary is entered as 2r11001.01 and displayed as 2ɽ11001.01. As well, radix numbers can be written with an exponent. Note however that the radix applies to the exponent as well. Thus 4ɽ1.22℮10, entered as 4r1.22℮10, evaluates to 416 because 10 is 4 in base 4. Contrast this with the similar-looking but very different manifest expression 4ɽ1.22⋅4^10, which evaluates to 1703936.

When the radix is greater than 14, the letters “e” and “E” become valid radix digits, rendering them unavailable to introduce an exponent. For this reason, a third exponent glyph “℮” is used to introduce an exponent. Contrast the input form 16ɽbcde10 of 16ɽbcde10 with the input form 16ɽbcd℮10 of 16ɽbcd℮10.

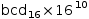
Radix digits are limited by the alphabet. Digits for number bases above 36 cannot be represented by the syntactic techniques described here.

Boolean values are a façade for real values 0 and 1. They are displayed as ⊤ for true and ⊥ for false. Boolean values are produced by comparison and containment operators, whose operands can be of any type. They are also produced by Boolean operators, whose operands are Boolean.

Complex numbers have both a composite form (see §2.3.2.3) called “complex-I” and a simple form called “complex-J”. The latter has the notation ⅉ and for the most part acts just like any other real constant except that it cannot, of course, be evaluated. However, the product ⅉ⋅ⅉ simplifies to -1. This idea extends to non-negative integer powers of ⅉ.

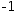
Mathematicians make extensive use of special values called named constants. The named constants supported by Myron are given in Figure 2.15. Named constants remain unchanged during simplification but their approximate value will be used during evaluation.

Symbol	Name	Description
ℼ	pi	ratio of circumference to diameter
ⅇ	Euler's Number	the base of the natural logarithms
ⅉ	√(-1)	Complex-J
ℽ	Euler–Mascheroni constant	the limiting difference between the harmonic series
∞	Infinity	represents computationally infeasible large numbers
¿	Indeterminate	represents computationally unobtainable values
⊤	True	produced by manifest Boolean expressions
⊥	False	produced by manifest Boolean expressions
ĉ	constant	the constant of integration

2.3.2.2 Strings

Strings are immutable sequences of characters. They are entered by enclosing the sequence in quotation marks. A small number of special characters are escaped by the backslash character: newline, quotation mark and backslash itself.

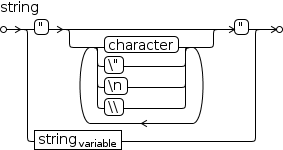
Strings can be composed by concatenation and partitioned by ↑ (substring) and ↓ (inverse substring, i.e, remove substring). They can be indexed and their length can be determined by the cardinality operator.

2.3.2.3 Composites

Composites are composed of other expressions. The general literal form consists of a comma-separated list of component expressions in parentheses followed by a suffix -- one of ⅈ, ɼ, ƈ or ʋ -- to indicate a complex-I, radial, column-vector or row-vector value. For ease of expression entry, alternative suffixes are also allowed: i, c, r or v. Complex-I and radial components must be real. Vector components can be real or complex-I, collectively scalar.

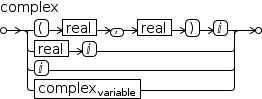
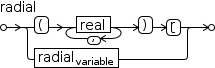
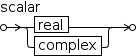
The display form of these values differs from the input form. Here are some examples of composite values: (1,2)ⅈ is the complex value (1, 2)ⅈ, (1,2)ɼ is the radial value (1, 2)ɽ, (1,2,3)ƈ is the column-vector value (1, 2, 3)ƈ and (1,2,3)ʋ is the row-vector value (1, 2, 3)ʋ.

Complex-I literals written in the general form must contain exactly two reals. Syntactic variations support the notation found in mathematics textbooks. A number or parenthesized expression followed by the ⅈ symbol is shorthand for a complex value with a zero real part. The symbol ⅈ by itself means a complex value with a zero real part and unit imaginary part. The display of complex literals depends on particular values of the real and imaginary parts, again to support the notation found in textbooks. Examples are given in Figure 2.18. More detail on composite values is given in §2.7.

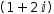
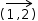
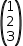
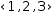
Input form	Simple form	Display form
(0,0)i	0i	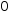0ⅈ
(0,1)i	1i	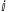ⅈ
(0,2)i	2i	2ⅈ
(1,1)i		(1, 1)ⅈ
(1,-1)i		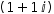(1, -1)ⅈ
(1,0)i	1	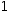(1, 0)ⅈ

Radial literals consist of a magnitude and at least one angle. A single-angle radial can be interpreted as a polar coordinate and a two-angle radial can be interpreted as a spherical coordinate.

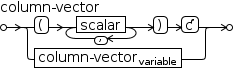
2.3.2.4 Collections

Collections (Figure 2.19) are general-purpose values that contain other values. Myron collections are tuples, sets and matrices. Tuple and set literals are entered by enclosing comma-separated lists of expressions in parenthesis (for tuples) or braces (for sets). Matrix literals are entered as comma-separated lists of tuple literals enclosed in brackets. Examples of each: (1,2,3) is the tuple (1, 2, 3), {c, d, h, s} is the set {c, d, h, s} and [(1,b,c),(d,e,f)] is the matrix [(1, b, c), (d, e, f)]. Tuples, sets and matrices can also be entered as tuple literals followed by one of the cast operators ʈ, ʂ or ɱ (or the alternative t, s or m); the cast is applied immediately. The previous three examples can thus be entered as (1,2,3)t, (c,d,h,s)s and ((1,b,c),(d,e,f))m. See §6.2 for notes on working with collections; see §2.4.3 and §2.10.2 for notes on the cast operator.

Generators are expressions that summarize collection values. See §2.8.3 for notes on generators and see Figures 2.44, 2.46 and 2.47 for the syntax of collection values and generators.

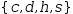
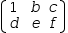
Like other values, a collection can be associated with a variable.

Mathematicians make use of special variable names that are used to refer to special sets that characterize numbers. These are given in Figure 2.20. The can be used with the set-inclusion operator ∈ to determine if a real meets some criterion.

∀n:n∈ℕ⇒(n=0)∨(n-1∈ℕ)

 

∀z:z∈ℤ⇒(z∈ℕ)∨(-z∈ℕ)

 

x∈ℙ

 

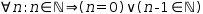
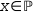
Symbol	Description
ℙ	the set of positive prime numbers
ℕ	the set of natural numbers (non-negative integers)
ℤ	the set of integers, positive, negative and zero
ℚ	the set of rational numbers
ℝ	the set of real numbers
ℂ	the set of complex numbers